Understanding Convolutional Neural Networks (CNNs) in Deep Learning

by Amit Prakash, on 03/11/2024

Convolutional Neural Networks (CNNs) are a specific type of neural network especially effective for tasks involving image data. CNNs excel at image classification, object detection, facial recognition, and other computer vision tasks due to their ability to capture spatial and temporal dependencies in images through specialized layers. This article dives into the structure, components, and operation of CNNs in-depth, providing insights into the fundamental layers and parameters that make CNNs a powerful tool in deep learning.

1. What is a Convolutional Neural Network?

Convolutional Neural Networks (CNNs) are a type of neural network that processes image data. They use special layers called convolutional layers to find important features, like shapes and textures, in images. These layers allow the neural network to easily understand how different parts of an image relate to each other.

A CNN is not fundamentally different from a feedforward network, it's main differences lie in its use of convolutional layers, which are at the heart of CNNs. Other layers have been introduced to facilitate easier training, but aren't the main focus of CNNs.

There have been many other networks inspired by CNNs, and there's not one architecture which is the de facto standard for a CNN. We will be exploring a variant the VGGNet, which is the network presented as the CNN in many other articles.

Other CNN Applications

CNNs have revolutionized computer vision and made deep learning mainstream. They've been employed in:

• Image Classification: Assigning categories to entire images.
• Object Detection: Locating objects within images.
• Face Recognition: Identifying and verifying faces.
• Image Segmentation: Assigning labels to individual pixels for detailed scene understanding.

2. CNN Architecture and Layers

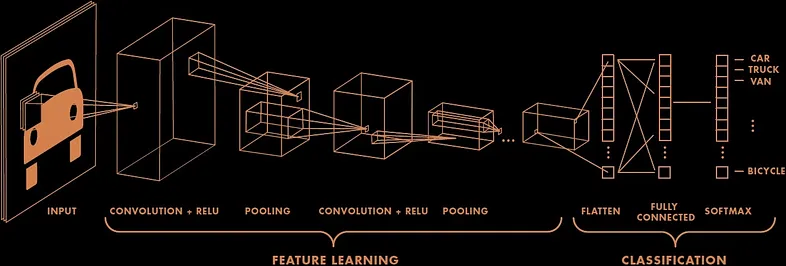
There are many variants of CNNs, but a common variant used for classification tasks has a pretty straightforward architecture. It consists of the actual convolutional layers, activation functions between each and pooling layers for downsampling. All of this is then flattened and passed to regular fully connected layers to a final layer having the classes. We'll be going through each layer in detail below.

Input Layer

The input layer in a CNN receives the raw image data, which is represented as a 3D matrix of pixel values (height, width, and depth, where depth usually refers to RGB channels). For example, a color image of dimensions 64x64 with three RGB channels would be represented as a 64x64x3 tensor. This layer standardizes the input for further processing by other layers.

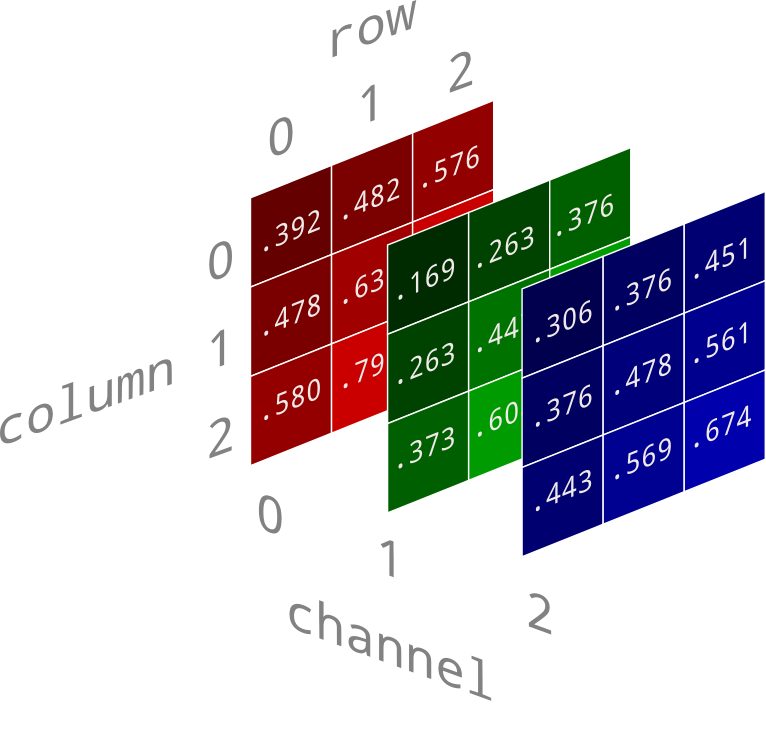
Convolutional Layers

Convolutional layers are at the core of CNNs. They are essential in allowing the model to recognize patterns in images.

They use filters, also called kernels, which are a small matrix (usually around 5x5 or smaller) containing values that the neural network can learn. These kernels are then overlayed over the image pixel by pixel and each pixel the kernel covers is multiplied by the value of the kernel at that pixel and added together. The sum is then output as the final pixel output.

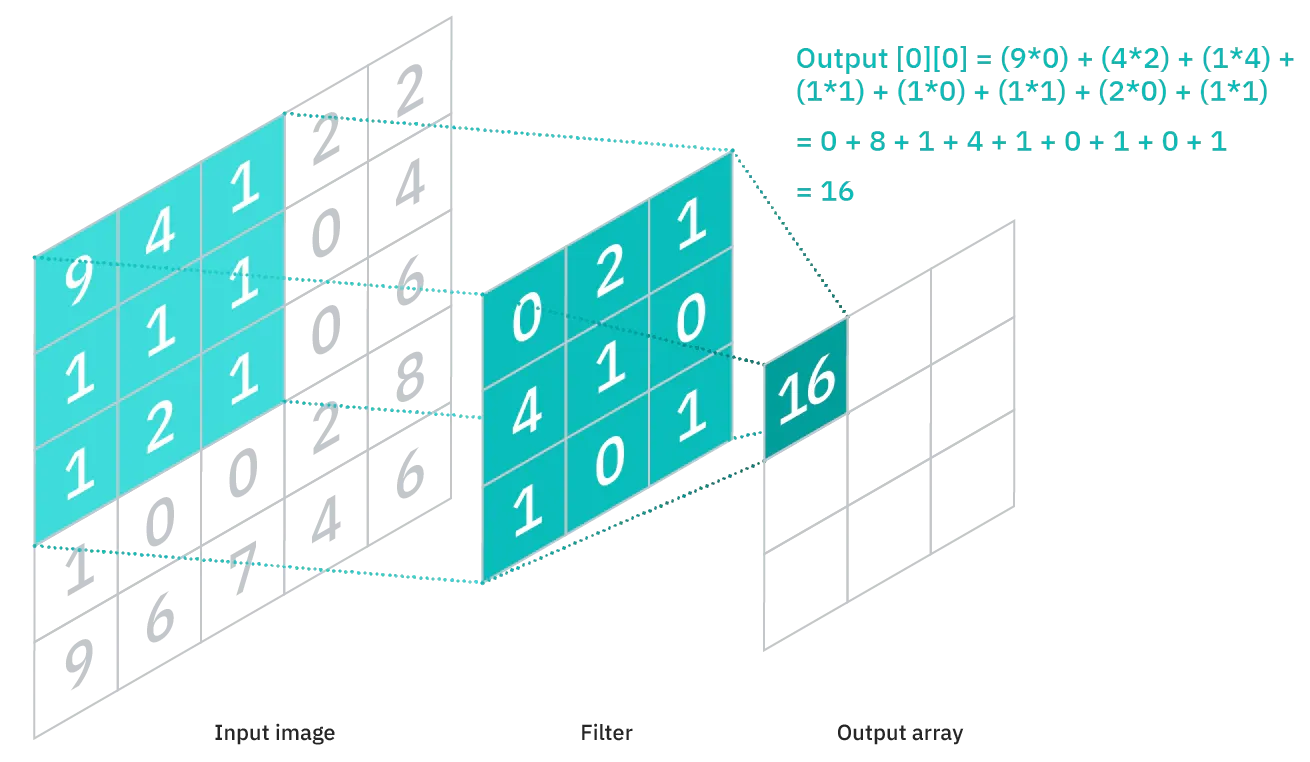
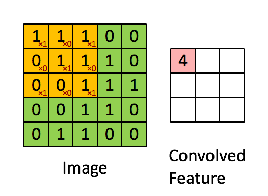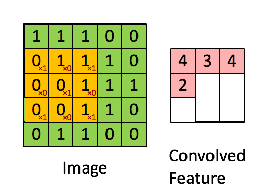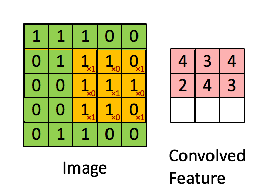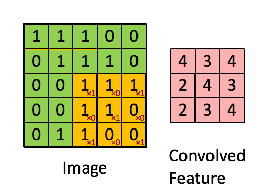
Let's take an example of a kernel which can detect vertical edges.

$$\left[\begin{array}{ccc}+1& 0& -1\\ +1& 0& -1\\ +1& 0& -1\end{array}\right]$$

Convolving this kernel with an image is equivalent to going to every 3x3 patch on the image, and taking the kernel and the pixel underneath it, multiplying them together and adding it. This kernel detects vertical edges, this can be seen by the fact that if you take a patch of pixels and the values on the left and right are the same, they cancel each other out, whereas if they are different, you get a non-zero value, hence giving an output image which is bright wherever there is a vertical edge.

If you're curious about manually created filters like these, look into edge detection. The example presented here is of a Prewitt filter, named after Judith M. S. Prewitt.

Now, just a single kernel wouldn't do much. So instead, we create as many filters as we need for our task. Each filter is applied to the image and we get a unique image from that filter. We can consider each of the unique images generated by these kernels as a channel, like your RGB color channels. So, each kernel generates its own channel, and we can apply a kernel to each channel to get another channel of images.

Now, the channels here are not your regular color channels where each represents the redness or blueness of your image. In a CNN, the early layers might be interpretable, but the deeper layers can have channels which contain much more complex signals. For example, a kernel at a point may be the "fur" channel, where the pixel is bright when that area might be fur, and dark if it isn't, so it's not possible to imagine them like regular color channels.

But this is the power of CNNs, they allow the model to learn patterns in images which would otherwise take extremely long if you trained them using linear layers.

There's still one thing we haven't covered, what do these models actually learn, where are the weights? Well, the weights here, which you might have guessed are the kernels themselves. we let the model learn the kernels which are best suited for it to detect features. These features may not be obvious to us, and they might not be ideal as they are learnt to minimize the loss throughout the model, and not just a single layer. So if you just analyze one of these layers, it's very unlikely that you'll find anything that resembles the Prewitt filter we looked at.

Stride and Padding

Two essential parameters in the convolution process are stride and padding.

• Stride: This is the number of pixels by which the filter moves across the image. For instance, a stride of 1 moves the filter one pixel at a time, while a stride of 2 moves it two pixels at a time, resulting in a smaller output feature map.

Input Size:

Padding:

Kernel Size:

Stride:

Input (5, 5)

After-padding (5, 5)

Output (4, 4)

 

Hover over the matrices to change kernel position.

• Padding: Padding adds extra pixels around the border of an image. Most libraries allow you to add padding by pixel to manually control the output shape, or they provide keywords like:
  • Same padding: Adds padding evenly on each side of the image so that the output of the convolution is the same shape as the input.
  • Valid Padding: This is the same as no padding as it drops any kernel which cannot cover the image.

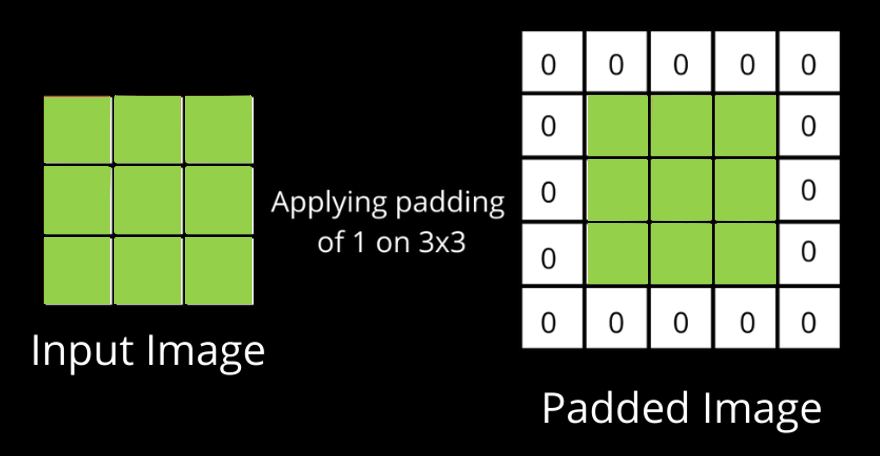
Why is Padding used?

Padding helps preserve spatial dimensions, ensuring that the output feature map has the same height and width as the input image. It also helps capture features at the edges of the image, which might otherwise be missed due to the filter size.

3. Pooling Layers

Pooling layers downsample feature maps, reducing spatial dimensions and computational load while preserving essential features. Pooling typically follows convolutional layers, shrinking the data while keeping the most critical aspects intact.

Types of Pooling

Pooling operations can be of various types, with the most common being:

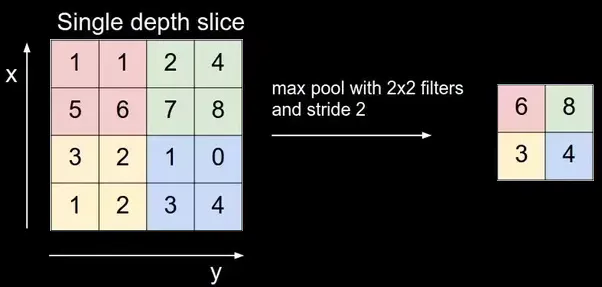
• Max Pooling: Selects the maximum value in a specific region, preserving the most prominent features.
• Average Pooling: Averages the values within the pooling window, preserving broader information.
• Sum Pooling: Sums all elements within the pooling window.

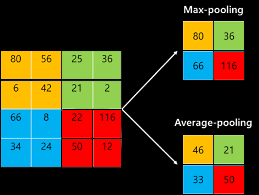
Example of Max Pooling: If using a 2x2 kernel with stride 2, max pooling would look at non-overlapping 2x2 regions in the feature map and pick the maximum value in each region. This approach reduces the map size by 75%, making the network more computationally efficient and less prone to overfitting.

Pooling reduces feature map dimensions, making models faster and more efficient, especially with large images, while retaining core information.

4. Fully Connected (FC) Layers

The fully connected (FC) layer is a traditional neural network layer where each neuron is connected to all neurons in the previous layer. It takes the flattened output from the final convolutional or pooling layer and combines these features for classification.

Flattening and Classification

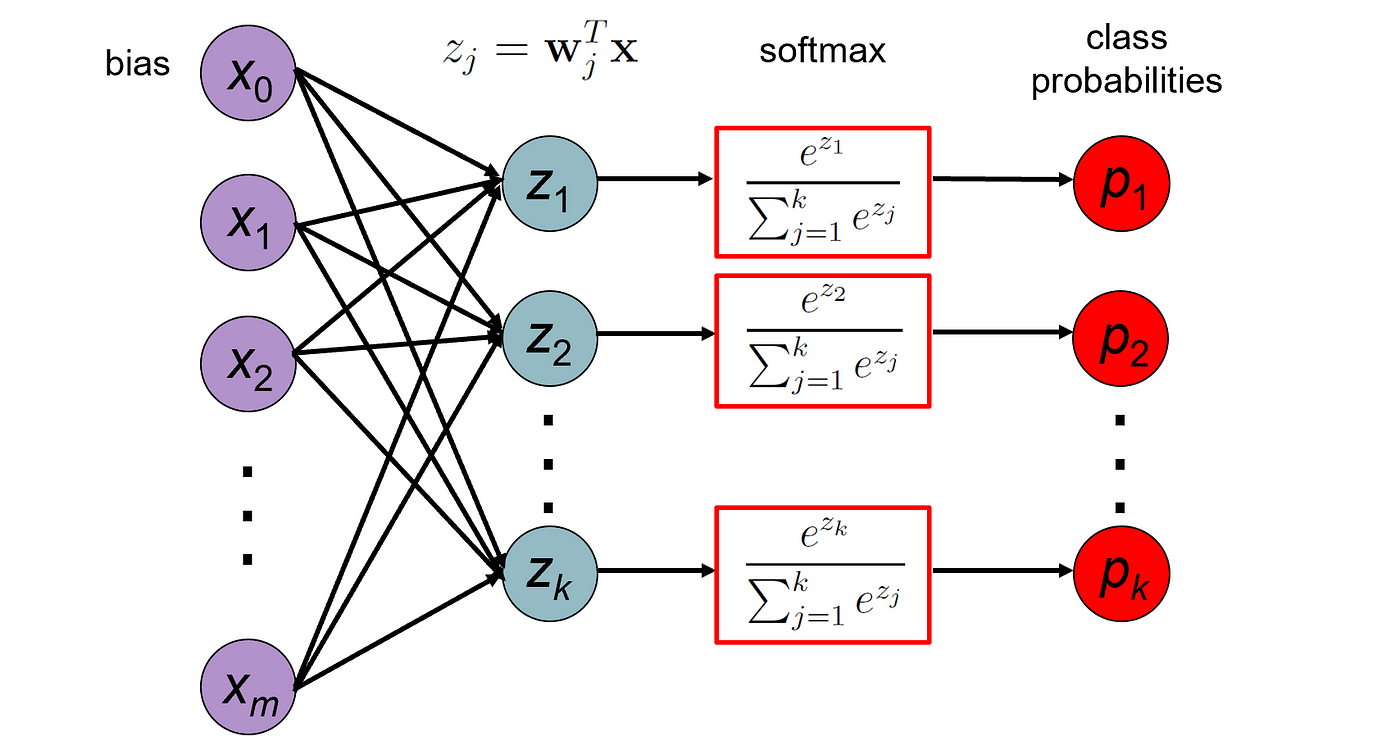
After the final pooling layer, the data (now in 2D) is flattened into a 1D vector. This vector is passed to the FC layer to map learned features to output classes. An activation function, such as softmax, is typically applied in the output layer to generate class probabilities. Softmax Function: Softmax transforms the output into probabilities that sum to 1, making it suitable for multi-class classification tasks. Each value represents the likelihood of the image belonging to a specific class.

$$\sigma {(\overrightarrow{z})}_i=\frac{e^{z_i}}{\sum _{j=1}^K{e}^{z_j}}$$

5. CNN Hyperparameters

Tuning hyperparameters is crucial to optimize CNN performance for specific tasks and datasets. Key hyperparameters include:

• Kernel Size: The dimensions of the filter (e.g., 3x3 or 5x5). Smaller kernels capture local details, while larger kernels capture broader features.
• Stride: Affects the feature map size, with larger strides producing smaller maps.
• Padding: Impacts the output size and ability to learn from border pixels. Zero-padding conserves more data at the edges.

6. Example CNN Architectures

Some well-known CNN architectures are designed to tackle specific challenges in image processing:

• AlexNet: Popularized CNNs for image classification with a deeper, larger network capable of handling complex data.
• VGGNet: Known for simplicity and uniform 3x3 filters, this network stacks more layers to improve depth.
• GoogLeNet (Inception): Utilizes inception modules with multiple filter sizes, allowing complex features extraction at different scales.
• ResNet: Introduces skip connections to alleviate the vanishing gradient problem, enabling very deep networks.

These architectures exemplify the evolution of CNNs, with each contributing innovations to handle larger datasets and improve accuracy.

A common structure of a CNN Classifier

1. Input Image: The network receives an image represented as an $height\times width\times channels$ matrix of pixels.
2. Convolution Layer: Applies filters to the image to produce feature maps, capturing essential spatial patterns.
3. ReLU Activation: Adds non-linearity to help the network learn complex patterns.
4. Pooling Layer: Downsamples the feature maps, reducing spatial dimensions.
5. Additional Convolutional and Pooling Layers: Layers are added to improve feature extraction, with each layer learning more abstract patterns.
6. Flattening: Converts the 2D matrix into a 1D vector, preparing it for classification.
7. Fully Connected Layer: Combines features to classify the input image.
8. Output Layer: A layer of size equal to the number of classes. Softmax is usually used to turn these into probabilties.

Conclusion

Convolutional Neural Networks have become a cornerstone of modern computer vision due to their ability to process and learn from image data effectively. By combining layers designed to capture spatial hierarchies and non-linear features, CNNs excel in tasks that involve complex data patterns. With improvements in architectures like AlexNet, VGG, GoogLeNet, and ResNet, CNNs continue to evolve, offering powerful solutions across a variety of fields. This architecture empowers machines to see, interpret, and act on visual information, pushing the boundaries of AI in image recognition and beyond.